Vektorji in kosinusni izrek

Test vektorji in rešitve dijakinje Nuše K

Test in rešitve dijakinje Nuše K

Dana sta vektorja 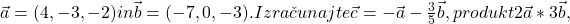$\vec a=(4,-3,-2) in \vec b=(-7,0,-3). Izračunajte \vec c=-\vec a-\frac{3}{5}\vec b, produkt 2\vec a*3\vec b,$ enotski vektor..kot med vektorjema…
Rešite iracionalno enačbo $\sqrt(x+5)= \sqrt(2x+17)-\sqrt(x)$
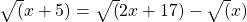
Vektorja 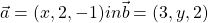$\vec a=(x,2,-1) in \vec b=(3,y,2)$ sta med seboj pravokotna, dolžina vektorja a pa je enaka 3. Izračunajte x in y!
Izračunajte $(9+4\sqrt5) (2-\sqrt5)^2+\sqrt(9^(^\frac{3}{2}^)-2)-0,25^(^-^0^,^5^) +\frac{3\sqrt10}{(4\sqrt5-5\sqrt2)}=$
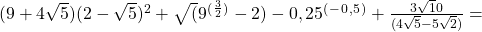
V paralelogramu ABCD ( a= 8 cm, b= 5 cm in alfa= 48°14` ) izračunajte dolžino diagonale e ( na 3 mesta) in dolžino višine na b na desetinko cm natančno!
Točke A(3,-1,2), B(-2,4,4), C(0,0,-5) so oglišča trikotnika.
Izračunajte koordinate razpolovišča stranice a in točko M, če velja CM : MB = 2:3.