- a) Odvajajte
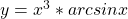
b)}{\sqrt[3]{x^-^2}}dx=](https://www.andrejruter.com/wp-content/ql-cache/quicklatex.com-013d424c371ac2476e2589bc52cb5d79_l3.png)
c)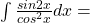
- Iz družine funkcij F(x)=
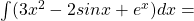 izberite tisto, ki ima začetno vrednost 5.
izberite tisto, ki ima začetno vrednost 5. - Zapišite enačbo normale na graf funkcije
![Rendered by QuickLaTeX.com f(x)= \sqrt[2]{1-2x}-3](https://www.andrejruter.com/wp-content/ql-cache/quicklatex.com-238b8b777b3c1907297a2601b37bf845_l3.png)
v njeni ničli! - Dana je funkcija f(x)= sin 3x + 4 cos x.
a) Izračunajte njen odvod in dokažite….
b) Ali funkcija v točki z absciso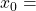 π/6 narašča ali pada? Odgovor utemeljite.
π/6 narašča ali pada? Odgovor utemeljite. - Določite prevojne točke, ter intervale konveksnosti in konkavnosti
f(x) = ( 2x-1)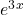 .
. - Zapišite enačbo tangente na krivuljo
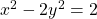 , ki je vzporedna premici x-y=5. Vse narišite!
, ki je vzporedna premici x-y=5. Vse narišite! - Pod kolikšnim kotom seka graf funkcije f(x) = 3 ln
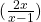 abscisno os? Zapišite definicijsko območje funkcije f(x).
abscisno os? Zapišite definicijsko območje funkcije f(x). - Izračunajte z diferencialom
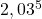 .
.