Rešeni primeri dijakinje NK
- Izmed treh inženirjev in 7 tehnikov je treba sestaviti komisijo 2 inženirjev in 3 tehnikov. Na koliko načinov je to mogoče:
a) če je lahko vsak član komisije,
b) če mora biti inž Janez v komisiji,
c) če tehnika Peter in Pavel nočeta biti v komisiji. - Koliko različnih zlitin dobimo, če imamo pet kovin, ki jih lahko zlivamo po dve ali tri skupaj?
- V ravnini je 7 premic, izmed njih so si 4 vzporedne. Koliko presečišč največ določajo?
- Koliko kotov določa 10 premic ravninskega šopa?
- Na nekem sprejemu je bilo 15 medsebojnih predstavitev. Koliko ljudi se je srečalo?
- Zapišite peti člen v razvoju
![Rendered by QuickLaTeX.com (1-\sqrt[2]{a})^9.](https://www.andrejruter.com/wp-content/ql-cache/quicklatex.com-cdc480525ac0b43313aed2d973cedc64_l3.png)
- Poiščite člen, ki vsebuje
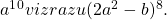
- Na krožnici s središčem v koordinatnem izhodišču je 8 točk, 3 v prvem kvadrantu in 5 v tretjem kvadrantu.
a) Koliko tetiv določajo?
b) …..
c)…. - Iz črk besede ZAGORJE sestavljamo “besede” s tremi različnimi črkami.
a) Koliko besed lahko sestavimo?
b) Koliko se jih začne na Z?
c)….
d)…
e)…. - Na koliko načinov lahko izmed 20 fantov in 8 deklic sestavimo šestčlansko ekipo v kateri naj bosta vsaj 2 fanta?
- Na koliko načinov lahko 5 vojakov razporedimo na tri stražarska mesta, tako da bo vsako mesto zasedeno z vsaj enim vojakom?
- Rokometni klub ima še sedem tekem do konca prvenstva. Na koliko načinov lahko igra, če planira 4 zmage, en poraz in dva neodločena izida?